En su libro Beyond Infinity (Más allá del infinito), la Dra. Eugenia Cheng explora el funcionamiento interno del infinito, un misterioso concepto que todos conocemos desde la infancia, pero que nunca hemos pretendido comprender, ya que parece estar reñido con nuestro propio cerebro finito. Hay hechos infinitos en el libro (bueno, bastantes, muchos, en cualquier caso), pero aquí es solo os explicamos una mínima expresión.
Infinito más uno
Imagina un hotel infinito con habitaciones numeradas 1, 2, 3, 4 y así sucesivamente y progresivamente. Incluso si tuviese lleno, siempre podría caber otro huésped más, pide a todos los huéspedes subir una habitación, dejando la habitación 1 gratis para el nuevo huésped. Sin embargo, esto causaría una molestia infinita, ya que todos los huéspedes tienen que cambiar de habitación. No sería ninguna molestia si el invitado extra llegase el primero. Esto demuestra que uno más infinito no es igual que infinito más uno. Shakespeare sabía esto dijo «Para siempre y un día«. Él debía saber que esto es más que meramente «para siempre«.
¿Mayor que infinito?
Algunos infinitos son más grandes que otros. El infinito más pequeño es cuántos números enteros hay: 1, 2, 3, 4 y así sucesivamente y en progresión. Si incluimos fracciones hay infinitamente más números. De hecho, hay infinitas fracciones entre cada número entero. Pero en general no hay más números a menos que incluyamos los números irracionales, los «decimales que duran para siempre«. Hay dos para el poder de la infinitud de aquellos, es decir, 2 x 2 x 2 … multiplicado infinitamente muchas veces. El matemático Georg Cantor demostró que esto es más grande que el infinito, cualquier tipo de infinito con el que empieces.
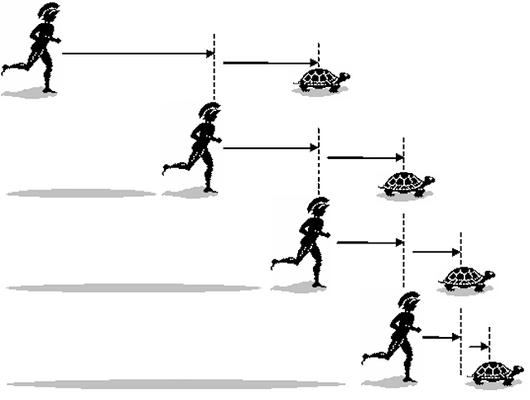
La paradoja de Zenón
Un día tiene solo un número finito de horas y un número finito de minutos, pero haces infinidad de cosas todos los días. Incluso para caminar hasta la nevera y cubrir un número infinito de distancias: primero hay que cubrir la mitad de la distancia, luego la mitad de la distancia restante, y la mitad de la distancia restante, y así sucesivamente progresivamente. Afortunadamente, puedes cubrir esas infinitas distancias en tiempo finito, de lo contrario estarías infinitamente hambriento. Esta es la paradoja de Zenón, y no se resolvió realmente hasta la invención del cálculo un par de miles de años después de la muerte de Zenón.
Otro mundo
Tú puede pensar que 1/0 es infinito. Pero no lo es. Pero también lo es. ¿Cómo pueden ambos ser verdad? Depende del mundo matemático en el que te encuentres. En el mundo de los números ordinarios, la división por cero no puede definirse. Si 1/0 tenía una respuesta, entonces todo se colapsaría a cero. Pero hay un mundo matemático llamado los números complejos extendidos en los cuales podemos definir 1/0 para ser infinito sin colapsar todo. Esto nos demuestra que las matemáticas no es todo sobre el bien y el mal, sino sobre la investigación de diferentes mundos posibles en los que diferentes cosas pueden ser verdad.

Relaciones complejas
Si fuéramos inmortales podríamos procrastinar para siempre. En realidad, hay una versión matemática de esto, que es un teorema que la Dra. Cheng ha demostrado. Su investigación se centra en la teoría de categorías de dimensiones superiores, que consiste en estudiar las relaciones entre las cosas, las relaciones entre las relaciones, las relaciones entre las relaciones entre las relaciones, y así sucesivamente. En dimensiones finitas tienes que parar en un cierto punto y decidir qué relaciones cuentan como equivalente. Esas decisiones son matemáticamente difíciles. Mientras que en dimensiones infinitas tu puedes posponer la decisión para siempre. Esto significa que la categoría dimensional infinita es más fácil de trabajar que la finita. Es satisfactoriamente raro.
Considérate infinitamente más sabio después de estos hechos fascinantes que explica el nuevo libro de Eugenia Cheng sobre este concepto matemático, el más curioso y el más bello de las matemáticas.